Today you’ll learn how binary subtraction works at the lowest level in your machine.
If you’re not familiar with binary check out binary part-0 here you’ll find out why binary is used and how it flows through components of your PC.
The 5 components in binary subtraction
In binary part-I, you used 5 components input A input B, Carry in, Sum and Carry out.
For binary subtraction Carry in, Sum, and Carry out, become Borrow in, Difference and Borrow out.
Input A. and B, remain a byte.
How subtraction happens in your CPU
You already know your CPU uses logic gates to perform bit-by-bit operations.
In subtraction we use a following combination of gates:
For Difference: ((a XOR b) XOR borrow_in)
And BorrowOut: (NOT(a) AND b) OR (NOT( a XOR b) AND borrow in)
Difference explained
Difference is used to return the output after applying a bit-by-bit operation.
When the operation is done; difference is used to store the remaining byte and give it in return.
ex. When you subtract 17 - 1 using the calculator on your phone, your CPU goes to work, starting at a transistor, each bit flows bit-by-bit through logic gates, each difference is stored and a byte is returned.
Now that we’ve covered what ‘difference’ means, let’s break it down and see how CPUs handle subtraction at the logic gate level.
Difference under the hood
Figure 1.0 displays the difference in a diagram using 2X logic gate XOR this is the exact route your CPU follows when transiting bits.
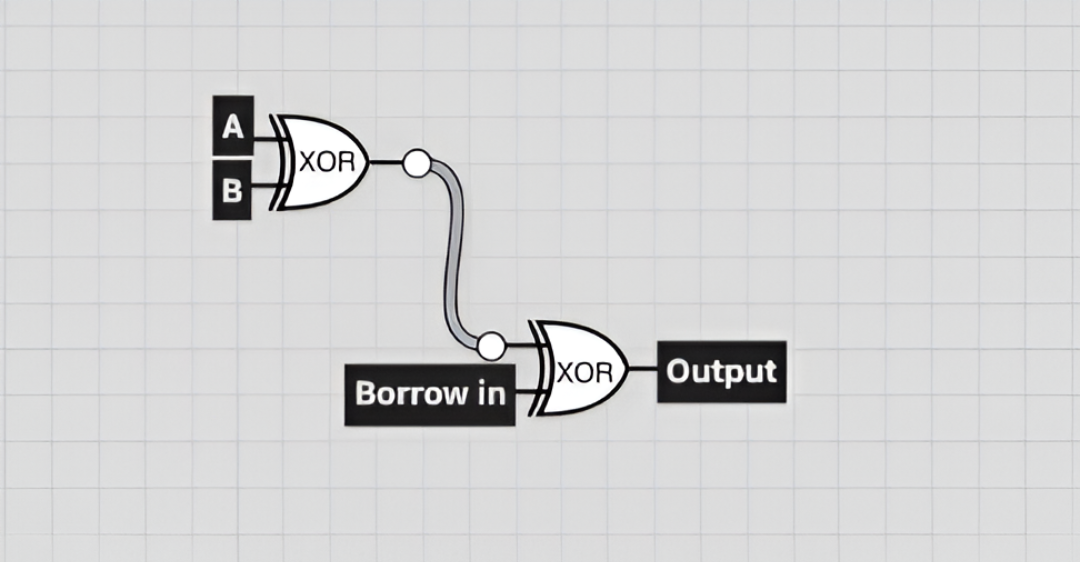
a < b OR Borrow out.
Bit A and bit B flow through the logic gate XOR which then returns a bit, that bit then flows to the next gate, XOR logic is applied again with Borrow in, and the final output is returned.
Why XOR is used in Difference
XOR is used to compare two bits, it returns 1 if the bits are different and 0 if they’re the same. That’s why it’s ideal for calculating the bitwise difference.
If you’re not familiar with XOR check out binary-part-I where you walk through a bit-by-bit XOR simulation using the basic gates, AND, NOT, and OR.
Now let’s move to borrow out.
Why Borrow out is needed
Because computers only store bits (0s and 1s) , going below 0 will cause underflow, which will cause us to borrow out.
Borrow-out checks whether subtraction at a bit column requires borrowing.
We need to borrow when input A is less than input B at that bit column.
How borrow out flows through your CPU
Figure 1.1 shows Borrow out in a circuit simulation, using for different gates NOT, AND, OR, and XOR.
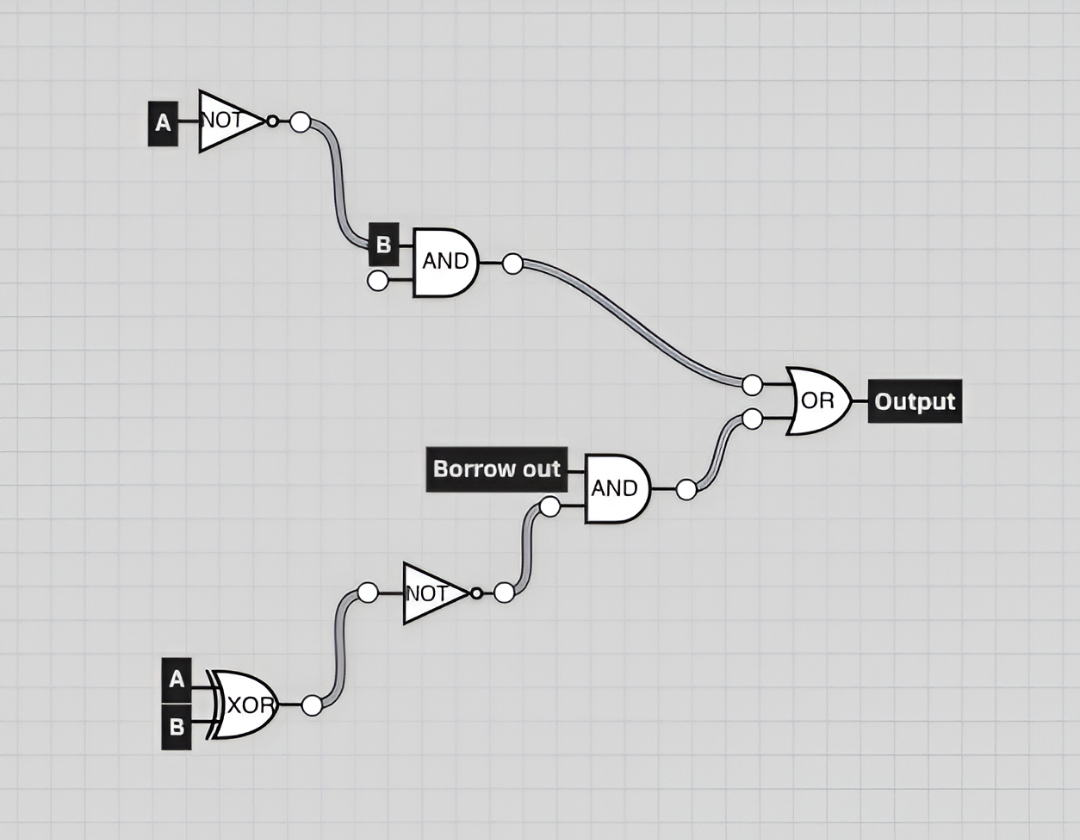
Starting at the top A flows through the NOT gate to the transistor of the AND gate where B is waiting together they flow through AND and a final bit is returned. If a bit is stored we need to borrow else we follow the next logic.
A and B flow through XOR a bit is returned which then flows through not borrow in is waiting at the transistor of the AND gate where both bits now flow through together, if the return value is 1 bit then we need to borrow if not we don’t.
Now you know how both Difference and Borrow out flow through logic gates lets walk through a table.
Full table walkthrough
Figure 1.2 shows a subtraction full 8 bit adder with all five components. On the left hand side each bit’s index position is shown.
| Bit Position | A | B | Borrow In | Difference | Borrow Out |
|---|---|---|---|---|---|
| Bit_0 | 0 | 0 | 0 | 0 | 0 |
| Bit_1 | 1 | 1 | 0 | 0 | 0 |
| Bit_2 | 0 | 1 | 0 | 1 | 1 |
| Bit_3 | 1 | 1 | 1 | 1 | 1 |
| Bit_4 | 1 | 0 | 1 | 0 | 0 |
| Bit_5 | 0 | 1 | 0 | 1 | 1 |
| Bit_6 | 0 | 0 | 1 | 1 | 1 |
| Bit_7 | 0 | 1 | 1 | 0 | 1 |
For this example let’s take the row of bit_2.
| Bit_A | 0 |
| Bit_B | 1 |
| Borrow in | 0 |
We start at calculating the difference so we know what to write down at the Bit_2 column's position, so ((0 XOR 1) = 1) XOR 0) = 1, and we now know 1 needs to be written down in the column of Bit_2.
Next, we check if a borrow is needed: (NOT 0 = 1) AND 1 = 1. This already signals a borrow, but let’s complete the logic. (0 AND (0 XOR 1)) = 0.
So, 1 OR 0 = 1, this confirms that borrow-out is 1.
Based on the math you’re using the CPU decides if it’s unassigned, if it’s unassigned mathematics then the CPU calls an error called underflow and a borrow out is needed.
If you’re using assigned math you'll simply go below zero using 2's complement.
What is 1’s and 2’s complement
Since memory only stores 0s and 1s, going below 0 directly isn’t possible without causing an error while compiling.
So if we need to represent a negative number, we use 1s complement and 2s complement.
1’s complement flips all bits, e.x. 10101 becomes → 01010, when you look at the pattern you simply see that all 1s have become 0s and all 0s have become 1s.
2’s complement flips all bits + adds 1 bit, e.x. 00110 becomes 11001 then one is added so it becomes 11010.
Closure
If you’re interested in Systems, Rust, Comp-sci, Blockchain, and more follow along. To stay tuned in on the blog check out: X/Twitter where I’ll be posting when a blog goes live.
If you want programmed example where i simulate logic using functions check out: binarySeries where I have built an ALU from the gates up.
That’s it for now, keep in mind, “every program is an ALU at its lowest level” till the next one.